扫雷

小明最近迷上了一款名为《扫雷》的游戏。

其中有一个关卡的任务如下：

在一个二维平面上放置着 $n$ 个炸雷，第 $i$ 个炸雷 $(x_i,y_i,r_i)$ 表示在坐标 $(x_i,y_i)$ 处存在一个炸雷，它的爆炸范围是以半径为 $r_i$ 的一个圆。

为了顺利通过这片土地，需要玩家进行排雷。

玩家可以发射 $m$ 个排雷火箭，小明已经规划好了每个排雷火箭的发射方向，第 $j$ 个排雷火箭 $(x_j,y_j,r_j)$ 表示这个排雷火箭将会在 $(x_j,y_j)$ 处爆炸，它的爆炸范围是以半径为 $r_j$ 的一个圆，在其爆炸范围内的炸雷会被引爆。

同时，当炸雷被引爆时，在其爆炸范围内的炸雷也会被引爆。

现在小明想知道他这次共引爆了几颗炸雷？

你可以把炸雷和排雷火箭都视为平面上的一个点。

一个点处可以存在多个炸雷和排雷火箭。

当炸雷位于爆炸范围的边界上时也会被引爆。

输入格式

输入的第一行包含两个整数 $n$、$m$。

接下来的 $n$ 行，每行三个整数 $x_i,y_i,r_i$，表示一个炸雷的信息。

再接下来的 $m$ 行，每行三个整数 $x_j,y_j,r_j$，表示一个排雷火箭的信息。

输出格式

输出一个整数表示答案。

数据范围

对于 $40\%$ 的评测用例：$0 \leq x,y\leq 10^9,0\leq n,m\leq 10^3,1\leq r\leq 10$，
对于 $100\%$ 的评测用例：$0\leq x,y\leq 10^9,0\leq n,m\leq 5 \times 10^4,1\leq r\leq 10$。

1
2
3
4
5
6
7
输入样例：
2 1
2 2 4
4 4 2
0 0 5
输出样例：
2

样例解释

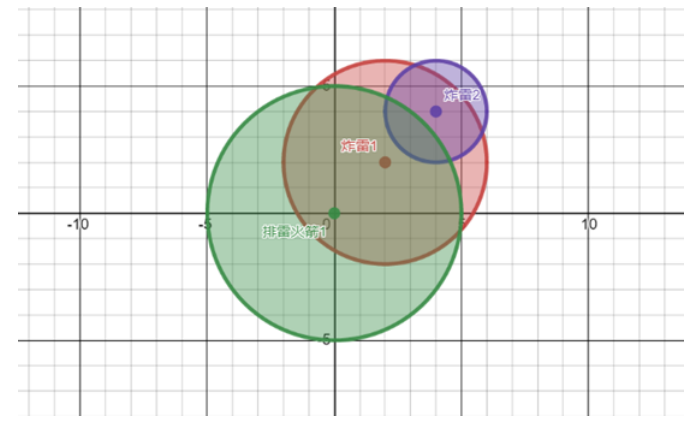
示例图如下，排雷火箭 $1$ 覆盖了炸雷 $1$，所以炸雷 $1$ 被排除；炸雷 $1$ 又覆盖了炸雷 $2$，所以炸雷 $2$ 也被排除。

扫雷

解题思路

这道题实际上是图的遍历问题，一个地雷如果能引爆另一个地雷，则连一条有向边。但是在本题中，最坏情况下可能有$100000 \times 50000$条边，显然会$TLE$、$MLE$；

我们需要做的是快速查找一个圆内有哪些地雷，因此我们可以使用哈希表来实现；

由于 $x,y\leq 1^9$ ，故哈希函数 $x \times 1^9 + y$ ，保证了所有点不会发生冲突；

由于圆的范围不好确定，故枚举矩形并加以判定即可；

此外，题目数据存在同一位置的多颗地雷，对于此，只需要存储最大半径即可。

哈希表空间越大，查找一般越快速，故本题可以开十倍空间

AC代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
#include <iostream>
#include <cstring>
#include <algorithm>

using namespace std;

typedef long long LL;

const int N = 50010, M = 999997,null = -1;

struct Circle{
    int x,y,r;
}C[N];

LL h[M];

int id[M];  //  表示哈希表中该位置存的是哪一个点(同一位置半径最大的点)
bool st[M];

int n,m,x,y,r;

LL get(int x,int y) {
    return x * 1000000001ll + y;
}

int find(int x,int y) {
    LL key = get(x,y);
    int t = (key % M + M) % M;
    while(h[t] != null && h[t] != key) t = (t + 1) % M;
    return t;
}


void dfs(int x,int y,int r) {
    for(int i = x - r; i <= x + r; ++ i)
        for(int j = y - r; j <= y + r; ++ j)
            if((x - i) * (x - i) + (y - j) * (y - j) <= r * r) {
                int t = find(i,j);
                if(id[t] && !st[t]) {
                    st[t] = true;
                    dfs(C[id[t]].x,C[id[t]].y,C[id[t]].r);
                }
            }
}

int main() {
    memset(h, -1, sizeof h);
    scanf("%d%d", &n, &m);
    for(int i = 1;i <= n; ++ i) {
        scanf("%d%d%d",&x,&y,&r);
        C[i] = {x,y,r};
        int t = find(x,y);
        if(h[t] == null) h[t] = get(x,y);
        if(!id[t] || C[id[t]].r < r) id[t] = i;
    }
    while(m--) {
        scanf("%d%d%d",&x,&y,&r);
        dfs(x,y,r);
    }
    int res = 0;
    for(int i = 1;i <= n; ++ i) {
        int t = find(C[i].x,C[i].y);
        if(st[t]) ++ res;
    }
    printf("%d\n",res);
    return 0;
}